|
|
Координатная плоскость
Специфика темы позволяет предложить материал в увлекательной форме. Иногда довольно сложные вопросы, связанные с координатами, удается объяснить почти в игровой форме. Идея координатной плоскости предполагает связь между некоторой фигурой и ее координатным представлением. Тема содержит два типа основных заданий: построение фигуры по ее координатному описанию и, наоборот, нахождение координатного описания фигуры по ее геометрическому заданию. При этом интересно работать не с абстрактными фигурами, а с изображениями знакомых предметов. Детям гораздо интереснее в результате выполнения задания получить изображение зверька, цветка или птицы. Я стараюсь использовать стилизованные рисунки строений, животных, растений и другие. С радостью и удовольствием учащиеся выполняют такие задания. С большим энтузиазмом ученики обычно встречают задания, в которых надо придумать фигуру и описать ее с помощью координат. В таких заданиях они имеют возможность не только показать математические знания, но и проявить свою фантазию, творческий подход к выполнению поставленных целей.
|
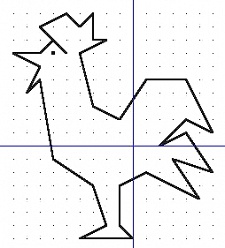
Петушок. Автор фигуры Макарьин Е., ученик 7 класса школы №9 г. Воронежа, 1994 год
Соедините последовательно точки:
(-5,7), (-7,9), (-5,10), (-4,9), (-3,10), (-3,8), (-2,8), (-4,7), (-3,3), (-1,2), (1,5), (4,5),
(6,1), (4,2), (2,0), (4,1), (6,-2), (3,-1), (5,-4), (1,-2), (-1,-3), (-1,-6), (0,-7), (-4,-7), (-2,-6),
(-3,-3), (-6,-1), (-7,5), (-8,4), (-7,6), (-9,7), (-7,7), (-6,8).
Глаз (-6,7). |

|
Цветок. Автор фигуры Гурова М., ученица 6 класса школы №9 г. Воронежа, 1996 год
Соедините последовательно точки:
(-1,-4), (-1,-7), (0,-8), (0,-3), (4,1), (5,4), (2,2), (0,-2), (0,5), (2,6),
(3,8), (2,10), (3,11), (2,13), (1,12), (1,11), (0,12), (0,13), (-1,12), (-2,14),
(-2,12),
(-3,13), (-4,11), (-3,10), (-4,8), (-3,6), (-1,5), (-1,-3),
(-2,0), (-5,3),
(-4,-1), (-1,-4). |
|
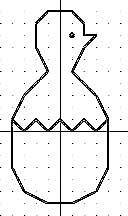
Цыплёнок. Автор фигуры Винокуров С., ученик 6 класса школы №9 г. Воронежа, 1996 год
Соедините последовательно точки:
(1,-6), (-1,-6), (-3,-5), (-4,-3), (-4,1), (-3,3), (-1,5),
(-2,7), (-2,9), (-1,10),
(1,10), (2,9), (2,8), (3,8), (2,7),
(1,5), (3,3), (4,1), (4,-3), (3,-5),
(1,-6), (-4,1), (-3,0),
(-2,1), (-1,0), (0,1), (1,0), (2,1), (3,0), (4,1).
Глаз (1,8). |
|
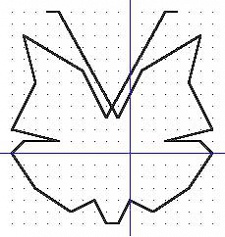
Бабочка. Автор фигуры Шкоткина Ю., ученица 6 класса школы №9 г. Воронежа, 1997 год
Соедините последовательно точки:
(4;12), (3;12), (-2;3), (-4;7), (-9;10), (-8;6),
(-10;2), (-6;1), (-9;1), (-10;0),
(-8;-3), (-5;-5),
(-3;-4), (-2;-6), (-1;-6), (0;-4), (2;-5), (5;-3),
(7;0), (6;1),
(3;1), (7;2), (5;6), (6;10),
(1;7), (-1;3), (-6;12), (-7;12). |
1
2
|






